Autor: Sergio Hidalgo
serhid@wired-weasel.com

Ejecutable y código fuente: SDLTest.zip

Introducción

En el último tutorial comenté cómo funcionaba el tilemapping “clásico”, en 2D. Ahora voy a empezar por fin con la representación isométrica, que supongo que es lo que más interesa.

La representación isométrica es un tipo de TileMapping, así que los conceptos en los que se basa son los mismos. Vamos a tener tiles, diferentes coordenadas (lógicas, absolutas, de pantalla), vamos a tener los procesos de plotting y mapping, etc...

Todos esos conceptos fueron lo que comenté en el otro tutorial. En este lo que explicaré es como se adaptan cada uno de ellos a este tipo de representación.

Por cierto, junto con el tutorial adjunto un pequeño programa de demostración. Podeis bajarlo desde el enlace del principio. El zip incluye el código fuente, pero necesitais tener la librería SDL configurada para compilarlo.

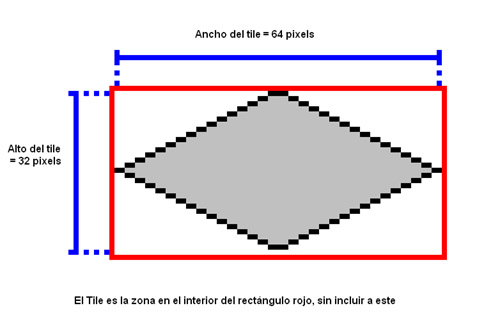
¿Qué es la representación isométrica?

Básicamente, consiste en sustituir los tiles cuadrados que usábamos antes por otros con forma de rombo. Con eso conseguimos crear una sensación de profundidad y añadir una tercera dimensión, pero sin todas las complicaciones de la programación 3D. (seguimos trabajando en 2D y con tiles, como siempre).

No voy a poner ninguna imagen de juegos isométricos porque creo que ya todos sabeis como son. Así que empecemos directamente. Un tile isométrico es tal que así:

Vale, cosas a tener en cuenta:

El tile es todo lo contenido en el rectángulo rojo, y no únicamente el rombo. Así que a la hora de ponerlos en un TileSet, es exactamente igual que si usasemos tiles rectángulares. Lo que será diferente es a la hora de componer el mapa con ellos.

La zona blanca en realidad estará rellena con el color transparente.

Tanto el alto como el ancho SON PARES. Esto es fundamental, porque al componer el mapa tenemos que hacerlo con una precisión de 1 pixel, perfecta, sin ranuras. Así que al hacer las divisiones por 2 que tocará hacer mas tarde no se puede “perder” nada.

El alto es la mitad del ancho. Esto es el “aspect ratio”, y no tiene porqué ser así. Un “alto” más grande dará la sensación de que lo vemos todo desde más arriba. Si es menor, pues al revés. En general, se suele usar la relación 2:1 en la mayoría de juegos.

Y lo último a tener en cuenta es que existe un “hueco”. La última fila de pixels está completamente vacía. Sería fácil decir que el alto del tile es entonces 31, y no 32. Bueno, esa fila está vacía por una razón: es la única manera de hacer que los tiles “encajen” entre sí.

Dependiendo de la forma del tile, puede que el hueco no esté debajo, sino a la derecha, arriba, o a la izquierda del rombo. Pero siempre hay un “hueco” en alguna parte.

Bueno, eso es todo. A partir de ahora usaré TILE_ANCHO y TILE_ALTO para las dimensiones.

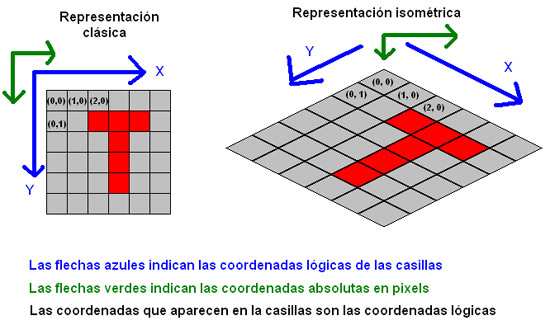
El Mapa

Vistos los tiles, vamos a ver como es un mapa isométrico:

Vale, lo primero que tenemos que tener en cuenta es que la representación lógica, el array de casillas aquel que hay en la memoria, no cambia en absoluto. Lo único que vamos a cambiar es la manera de dibujarlo.

Como se ve en el dibujo, las direcciones de los ejes de las coordenadas lógicas ya no coinciden con las de las coordenadas absolutas. Esto quiere decir que para hacer el plotting ya no basta con multiplicar, va a ser más complicado.

Por lo demás, es exactamente igual. Las dos representaciones son equivalentes. Y esto lo quiero recalcar mucho. Los conceptos son básicamente los mismos que usábamos, y el mismo mapa se puede representar por los dos sistemas.

Una cosa que quiero comentar, es que el origen de las coordenadas absolutas (las verdes) ya no está arriba a la izquierda del todo, como antes, sino que está arriba, pero en el centro. En realidad, esto es porque el origen de las coordenadas absolutas siempre está en donde esté la casilla (0, 0), y en la representación isométrica esta casilla está ahora arriba y en el centro.

Lo que viene a decir esto es que ahora tendremos coordenadas absolutas negativas (-50 pixels, por ejemplo), que antes no teníamos.

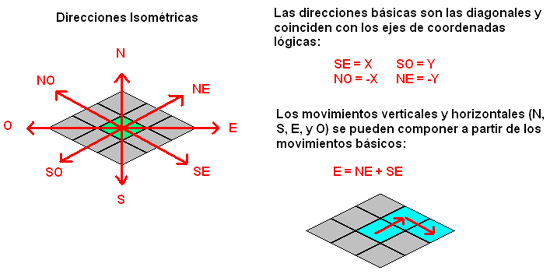
Tabla de Movimientos

Antes de meternos con el plotting, fórmulas y tal, quiero comentar una cosa que usaremos más adelante, la tabla de movimientos.

En un juego isométrico, si nuestro personaje está en (x, y) y se mueve a la casilla de “la derecha”, la coordenada de la nueva casilla no es (x+1, y), sino que será (x+1, y-1). Hablando siempre de coordenadas lógicas.

Como esto no es muy intuitivo, resulta útil construirse una función a la que le pasemos las coordenadas de la casilla, la dirección en la que nos movemos, y devuelva las coordenadas de la nueva casilla. De esta manera nos ahorramos tener que estar pensando como se hacía cada vez que necesitemos “desplazarnos” por las casillas. Esto es a lo que se llama “tileWalking”.

Para ello, vamos a dar un nombre a cada una de las direcciones en las que nos podemos mover. Normalmente se suelen usar los puntos cardinales:

Y a partir de eso, construimos la tabla:

Lo que tendremos entonces será una función “tileWalk” a la que le pasaremos como parámetro las coordenadas lógicas de una casilla, y la dirección. Esta función consultará la tabla y nos devolverá las nuevas coordenadas:

(x', y') = tileWalk (ISO_Direccion, x, y);

La dirección “ninguna” representa un movimiento nulo, por lo que nos quedamos en el sitio. La razón de incluirlo aparecerá más adelante.

Plotting

Las ecuaciones del plotting pueden parecer un poco raras si se miran de golpe, pero creo que se entienden bastante bien si miramos primero como afectan los cambios de las coordenadas lógicas a las absolutas:

No es tan raro, verdad?

PlotX se incrementa en TILE_ANCHO/2 si avanzamos por X, y se decrementa si avanzamos por Y
PlotY se incrementa en TILE_ALTO/2 tanto si avanzamos por X como por Y

Así que las “fórmulas” son estas:

plotX = (x – y) * (TILE_ANCHO / 2)
plotY = (x + y) * (TILE_ALTO / 2)

No estoy teniendo en cuenta el scroll, pero eso es exactamente igual que en los mapas clásicos. Basta con restar el desplazamiento a (plotX, plotY) para sacar las coordenada de pantalla.

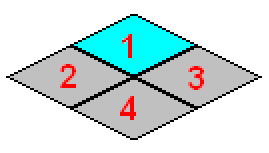
Orden de dibujado

Hay una cosa más que tener en cuenta a la hora de dibujar un mapa isométrico, y es que hay que respetar un cierto orden al dibujar las casillas. Dibujando solamente el “suelo”, que es lo que estamos haciendo ahora, da igual. Pero en cuanto metamos objetos a cada casilla habrá que tener cuidado, y dibujarlo todo en un orden en el que los objetos se tapen unos a otros de la forma correcta.

Básicamente, esto se conoce como el “algoritmo del pintor”, y consiste en que dibujamos desde “el fondo” hacia “delante”. De forma que un objeto que esté más cerca se dibuje después de otro que estaba más lejos, tapándolo si hace falta.

En la representación isométrica, los objetos que están “al fondo” son precisamente los que están más arriba en pantalla. Así que tendremos estas dependencias:

La casilla 1 debe dibujarse antes que la 2, la 3, y la 4
La casilla 2 debe dibujarse antes que la 4
La casilla 3 debe dibujarse antes que la 4
No existen dependencias entre las casillas 2 y 3

Con eso, tenemos 2 órdenes distintos para dibujarlas:

1, 2, 3, 4
1, 3, 2, 4

Y si extendemos estos órdenes a un mapa completo:

De momento, para no complicarnos, no voy a explicar aquí el orden “izq->der, arriba->abajo”, lo reservo para otro tutorial. Pero desde luego, a la hora de programar el motor, usaremos ese sistema, porque nos simplifica el meter la optimización básica de no dibujar el mapa completo, sino tan solo los tiles que aparecen en pantalla.

Y bueno, para ver una demostración de todo esto en acción basta con mirar el código fuente del SDLTest que adjunto. Excepto la tabla de movimientos, incluye todo lo demás. El orden de dibujado que usa es el de las diagonales, así que podeis ver cómo el bucle es exactamente el mismo que aparecía en el otro tutorial:

//Por cada casilla del mapa
for (y = 0; y < MAPA_ALTO; y++) {
   for (x = 0; x < MAPA_ANCHO; x++) {

      //Calculamos las coordenadas de pantalla a partir de las de la casilla
      //y el desplazamiento de la camara (scrollX, scrollY)

      px = (x - y)*(TILE_ANCHO/2) - scrollX;
      py = (x + y)*(TILE_ALTO/2) - scrollY;

      //Dibuja el tile en la pantalla
      blitTile (pantalla, px, py, mapa[x][y]);
   }
}

¿Y el MouseMapping?

Bueno, he explicado el tema del plotting, pero no he comentado para nada el paso inverso, convertir las coordenadas en pixels a coordenadas lógicas. Eso es porque en un mapa isométrico el mapping es más complicado que en los mapas cuadrados clásicos. Por eso lo voy a dejar para el siguiente tutorial.

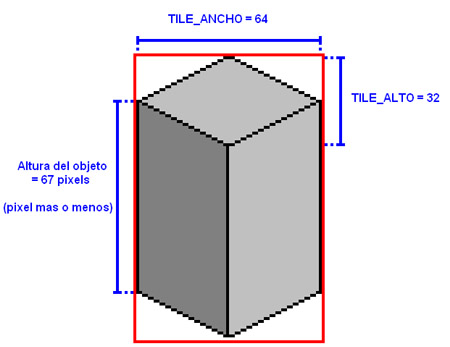
¿Y los objetos?

Pues sobre esto sí que voy a comentar:

Hasta ahora sólo hemos dibujado los “suelos”. Pero también tendremos distintos objetos, personajes, y paredes.

Bueno, la diferencia aquí es que los tiles de los objetos tienen un tamaño distinto a los tiles del suelo:

Este es el “bloque básico”. Cualquier objeto que dibujemos en una casilla estará “contenido” dentro de este bloque. Así que podemos tratar todos los objetos y personajes de la misma manera, asumiendo que son todos bloques básicos.

¿Y como hacemos para dibujar un bloque? Pues fácil, lo único que tenemos que tener en cuenta es que para alinear la parte de abajo del bloque con la casilla del suelo, hay que “moverlo” hacia arriba tantos pixels como alto sea el bloque (en este caso, 67).

Así que, sencillamente, restaremos 67 pixels a “plotY” cuando dibujemos un objeto, personaje, o pared. Y, por regla general, esto lo hará el propio tileset.

Y con esto termino por hoy. Un saludo.